Regression discontinuity is another statistical technique used to estimate the effect of a policy or other "treatment" when no experimental data are available.
To use a regression discontinuity (RD) design, we assume participants are assigned to treatment groups based on an observed variable (call this the assignment variable). In theory, participants with values of the assignment variable above a threshold are assigned to a treatment group, and those with values below the threshold are assigned to a control group (that is, they do not receive the treatment). Thus, treatment and control groups are not assigned randomly; we instead observe the measure underlying their assignment. The second crucial assumption is that the outcome variable is a continuous and smooth function of the assignment variable, especially near the threshold. There is no meaningful way to test this assumption, but in practice, a good theoretical justification combined with actual data plotted on a graph constitute convincing evidence that the assumption is well-founded.
Example
Suppose the poverty rate in a district is used to determine a school's eligibility for a specific policy intervention (the treatment). Thus, the poverty rate is the assignment variable, and the minimum poverty rate at which districts are eligible for the intervention is the threshold.
The assumption underlying RD is that the schools just above and just below the threshold poverty rate cutoff are very similar. The only assumed difference between these two groups of schools is that the schools above the minimum poverty rate are eligible and receive the policy intervention (treatment), whereas schools below the threshold do not receive the policy intervention. RD estimates the impact of the policy intervention by comparing the outcomes of schools above to schools below the threshold, assuming that the difference in outcomes is the impact of the intervention.
The graph below illustrates the method graphically, where a positive effect of eligibility is visible as a jump at the threshold in predicted outcomes, where outcomes (e.g., the number of high quality teachers) are modeled as a function of the poverty rate. Data points should be graphed along with fitted curves, so the plausibility of fitted curves is immediately obvious.
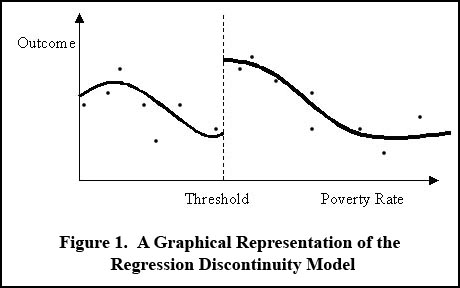
The RD estimate of the treatment effect (the gap at the dotted line in Figure 1) is measured by the estimate of the coefficient on a variable indicating values of the assignment variable above the threshold in a regression equation.1
RD's advantage over other quasi-experimental methods (such as instrumental variables) is the relative robustness of results to distributional assumptions and analysis methods. This is particularly true for our longitudinal data, where we can interpret the RD design as a kind of very sophisticated difference-in-difference estimator, and we can check directly if other potential confounders exhibit any change around the discontinuity.
OTHER CALDER RESEARCH METHODS
- Panel data models
- Hazard models
- Qualitative studies within a longitudinal data system
Notes
1. To test the robustness of the estimate, alternative specifications of the variables considered could be used including using non-linear terms for the indicator variable (either higher-order polynomial terms or categorical variables), or use techniques that put higher weight on neighboring observations to those at the cut point. Researchers can also assume different distributional assumptions for the underlying models, which would lead to using different regression techniques. To conclude that the RD design is appropriate, other variables for which no theoretical relationship to the observed variable is surmised (for example, the number of students in a school district) would also be plotted versus the assignment variable, along with a comparable set of regression results. If these irrelevant variables show no statistically significant jump at the threshold then the observed effect on the outcome variable is more plausibly traced to the treatment.



